| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- nuxt
- 프론트엔드
- 백준
- Beakjoon
- EC2
- 프로그래밍
- 우아한테크캠프
- 수업내용정리
- LIS
- 알고리즘
- Sequelize
- 오토마타
- BOJ
- 궁금증
- 14502
- 코딩감수성
- 직접연결하면안되는이유
- 오토마타정의
- JS
- DB관계
- 우테캠4기
- 14002
- 가장긴증가하는부분수열
- AWS
- 16918
- 코딩
- 코딩일기
- db
- 문제
- Backend
- Today
- Total
모든 경험을 소중하게
[BEAKJOON] 14502 - 연구소 본문
이번 포스트에서 다뤄볼 문제는 Beakjoon online judge 사이트에 있는 14502번 문제 연구소 이다.
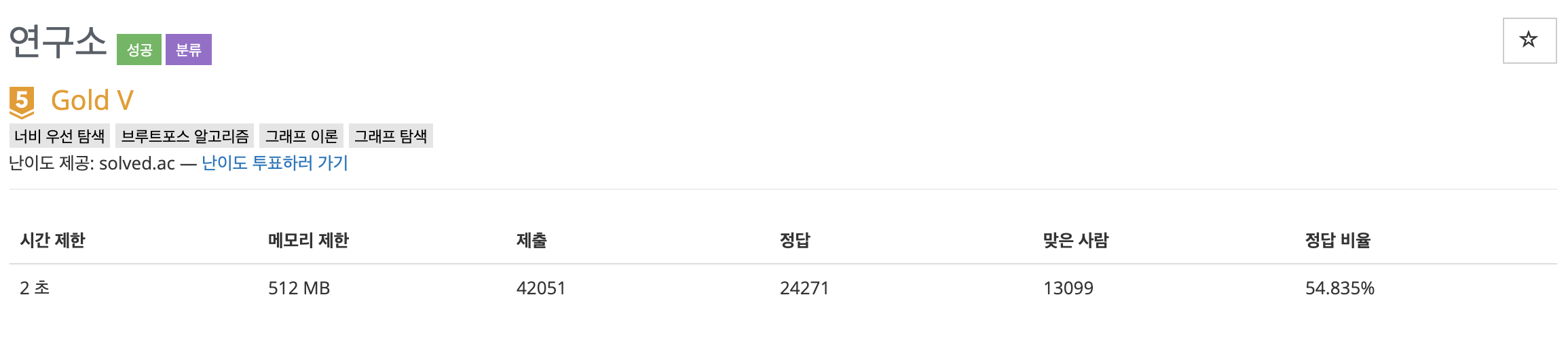
우선 시간 제한이 2초이므로, 그렇게 빡빡하지는 않다고 생각할 수 있었다.
문제를 마저 더 읽어보자.

새로 세울 수 있는 벽은 꼭 3개이다. 벽이 세워질 수 있는 곳은 0 값을 가지고 있는 좌표들뿐이다.
그렇다면, 어떻게 3개를 선택해야 가장 많은 0 을 남길 수 있을까?
문제를 마저 더 읽어보자.
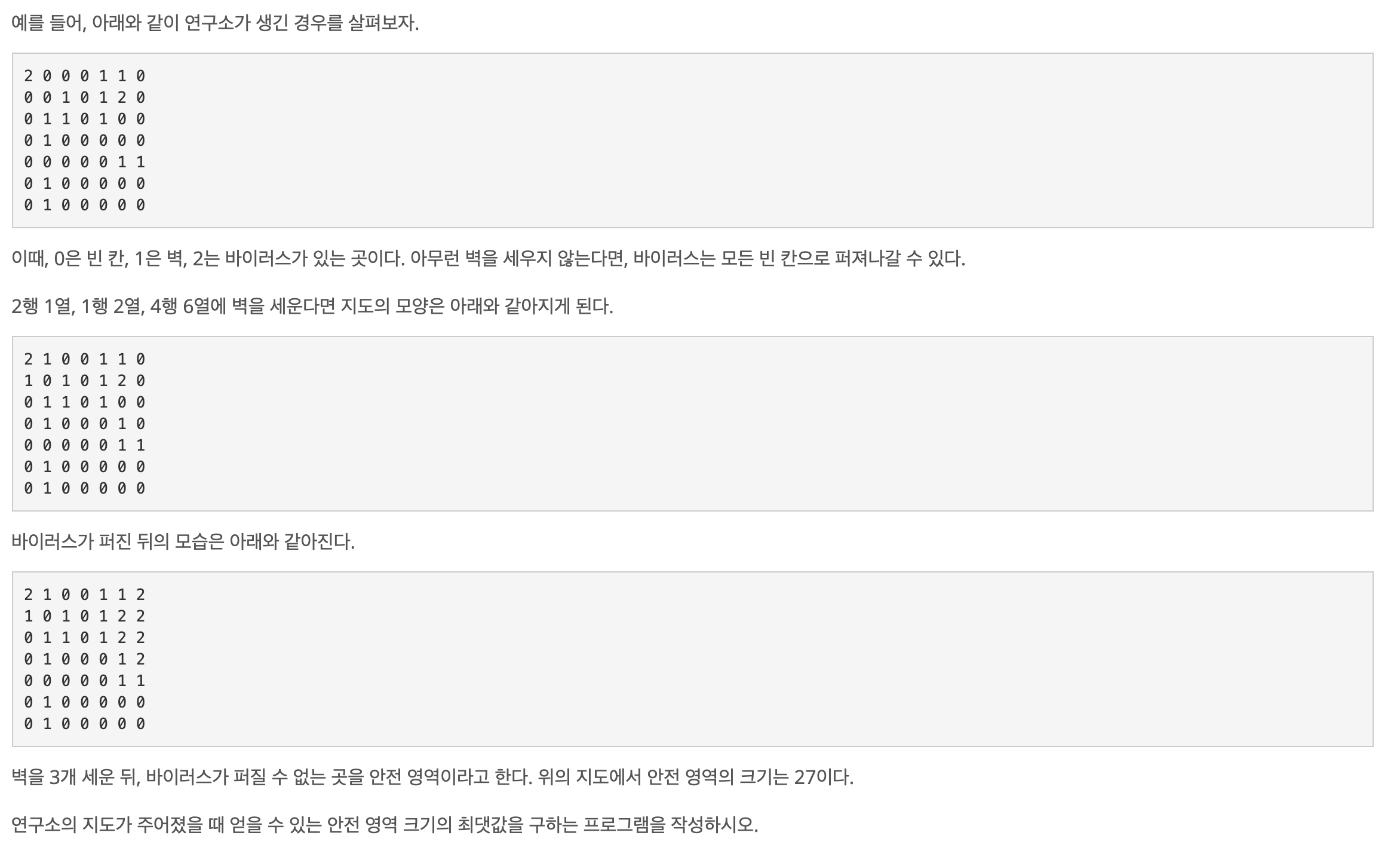
우선, 벽을 세운 후, 2인 점들을 queue 에 넣은 후, BFS 를 돌아야 안전 영역 ( 0 ) 의 크기가 몇일지 알 수 있는 것 같다.
따라서, 모든 벽 3개를 다 세워봐야만 안전 영역의 크기를 알 수 있다고 판단이 든다.
그렇다면, 0 을 가진 좌표 중 3개를 선택해야 하므로,
0의 갯수를 n 개라 했을 때, 경우의 수는 다음과 같다. nC3
nC3 = n * (n - 1) * (n - 2) / (3 * 2 * 1) => O(n^3)
따라서, n 에 따라 매우 값이 커질 수 있다. n 이 가질 수 있는 최대 값은 64개이다.
따라서, 시간 복잡도를 구해보면,
모든 경우의 수 x ( BFS + 초기화 ) 이다.
입력의 크기가 최대 8 x 8 이므로, 주어진 시간제한 내에 충분히 가능하다고 판단된다.
그렇다면 구현 해야 할 코드는 조합을 모두 구해내는 함수와 BFS 이다.
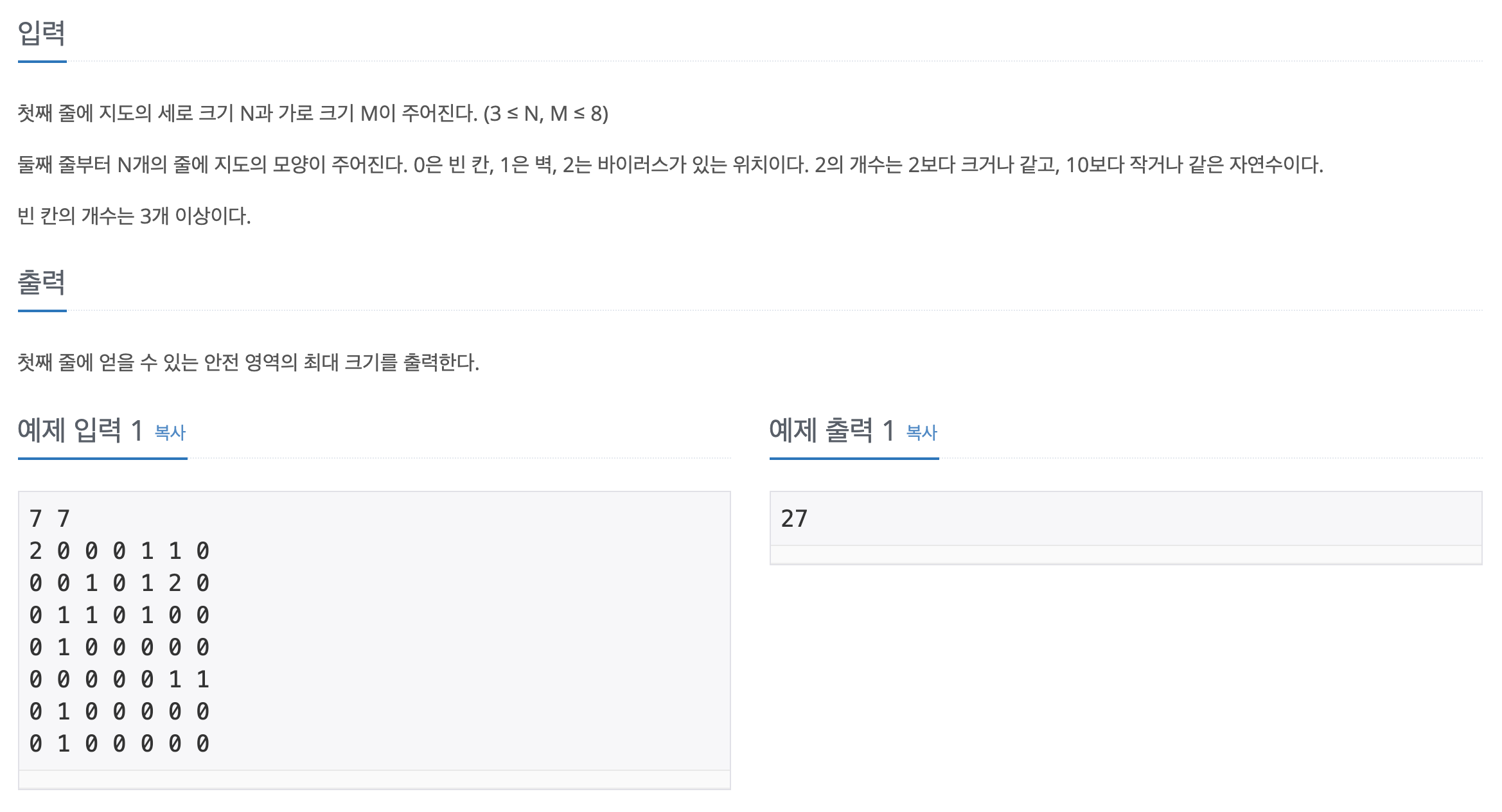
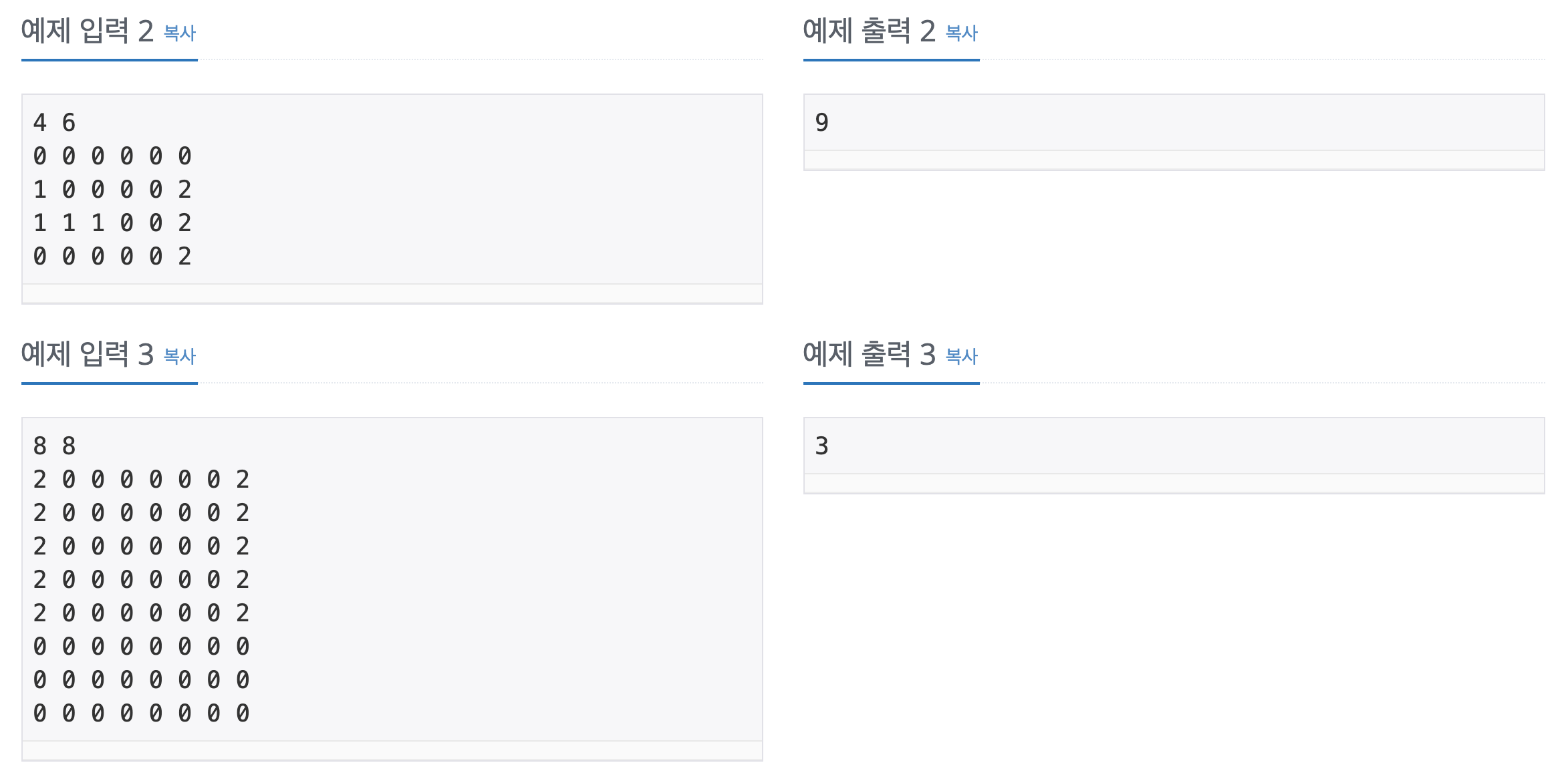
코드를 보려면 밑의 더보기 를 눌러주세요.
#include <stdio.h>
#include <vector>
#include <iostream>
#include <utility>
#include <queue>
#define MAX 8
#define Point pair<int, int>
#define Direction pair<int, int>
using namespace std;
// global variable;
vector<Point> virusArea;
vector<Point> safeArea;
vector<Point> dir {make_pair(0, -1), make_pair(0, 1), make_pair(-1, 0), make_pair(1, 0)}; // 상하좌우
int bfs(int map[][8], int n, int m, queue<Point > q);
int combination(int map[][8], int n, int m, int r, int idx, vector<int>& temp);
void solution(int map[][8], int n, int m);
bool isOutOfBounds(int x, int y, int R , int C);
int main(int argc, char const *argv[]) {
int n, m;
int map[MAX][MAX];
scanf("%d %d", &n, &m);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
int status;
scanf("%d", &status);
map[i][j] = status;
if(status == 0) safeArea.push_back(make_pair(i, j));
else if(status == 2) virusArea.push_back(make_pair(i, j));
}
}
solution(map, n, m);
return 0;
}
void solution(int map[][8], int n, int m) {
vector<int> temp;
int maxSafeArea = combination(map, n, m, 3, -1, temp);
printf("%d\n", maxSafeArea);
}
// combination(r, idx) : 벽을 r개 추가할 때, idx 번째 빈곳에 벽을 추가했을 때, 최댓값
int combination(int map[][8], int n, int m, int r, int idx, vector<int>& temp) {
int maxArea = -1;
if (idx == -1) {
for (int i = 0; i < (int)safeArea.size(); i++) {
temp.push_back(i);
int s = combination(map, n, m, r, i, temp);
maxArea = s > maxArea? s: maxArea;
temp.pop_back();
}
return maxArea;
}
if (r > 1) {
for (int i = idx+1; i < (int)safeArea.size(); i++) {
temp.push_back(i);
int s = combination(map, n, m, r-1, i, temp);
if (s > maxArea)
maxArea = s;
temp.pop_back();
}
return maxArea;
} else { // r 이 1일때
int cMap[MAX][MAX];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cMap[i][j] = map[i][j];
}
}
// safeArea 의 인덱스
for (int idx : temp) { // 새로운 벽을 copy 된 Map 에 추가
cMap[safeArea[idx].first][safeArea[idx].second] = 1;
}
queue<Point > q; // 독이 있는 점을 q 에 넣어준다.
for (Point vp: virusArea) {
q.push(vp);
}
// bfs 돌리고 0 의 갯수를 반환한다.
return bfs(cMap, n, m, q);
}
}
bool isOutOfBounds(int x, int y, int R , int C) {
return !(x >= 0 && x < R && y >= 0 && y < C);
}
int bfs(int map[][8], int n, int m, queue<Point > q) {
int count = 0;
while(!q.empty()) {
Point front = q.front();
q.pop();
for (Direction d: dir) {
int x = front.first + d.first;
int y = front.second + d.second;
if (!isOutOfBounds(x, y, n, m) && map[x][y] == 0) {
map[x][y] = 2;
q.push(make_pair(x, y));
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (map[i][j] == 0) count++;
}
}
return count;
}콤비네이션을 구현하기 위해서 재귀함수를 사용했다. 예전에 다른 블로그 글을 보면서 참고했을 때는 잘 와닿지 않았지만, 직접
짜보니까 재밌었다.
'Today I ... > algorithm' 카테고리의 다른 글
| [BEAKJOON] 14002 - 가장 긴 증가하는 부분 수열 4 (0) | 2021.05.12 |
|---|---|
| [BEAKJOON] 13335 - 트럭 (0) | 2021.05.01 |
| [BEAKJOON] 16918 - 봄버맨 (0) | 2021.04.27 |



